- معلم: أ.م.د. عثمان فريج
- معلم: أ. محمد مصطفى
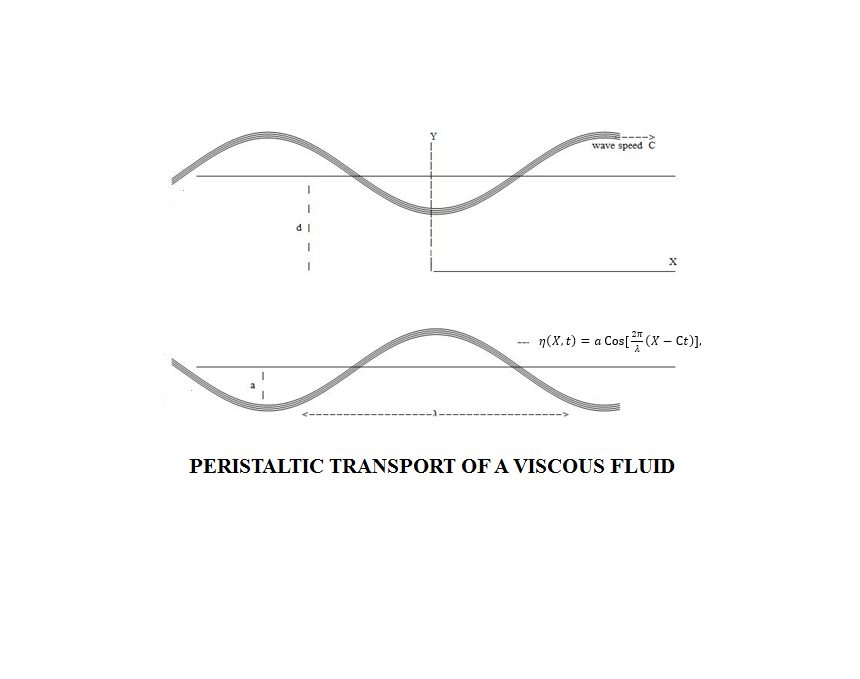
Biomathematics is the science that combines biology and mathematics to model and solve complex biological problems. It plays a pivotal role in advancing our understanding of life mechanisms and ecosystem dynamics by integrating mathematical theories with biological questions. It is concerned with the application of mathematical theories to the structure and function of living organisms. Moreover, biomathematics opens doors to innovative solutions in medicine and environmental sciences.
- معلم: د. محمد حسن هارون حسن
: هي نوع من المعادلات التفاضلية ، ( Partial Differential Equations ) المعادلات التفاضلية الجزئية
المعادلة التفاضلية الجزئية هي معادلة رياضية تحتوي علي مشتقات جزئية لمتغير تابع أو توابع بالنسبة لمتغيرين مستقلين أو أكثر .
تستخدم المعادلات التفاضلية الجزئية لصياغة وحل المسائل التي تتعلق بتوابع ذات عدة متغيرات مستقلة مثل تلك الموجودة في الصوت والحرارة والكهرباء الساكنة وتدفق الموائع والمرونة وغيرها ، حيث أنه من الممكن التعبير عن ظواهر فيزيائية مختلفة باستخدام معادلات رياضية متشابهة الصيغة.
وتعد مرتبةُ المعادلة order of equation هي مرتبةَ أعلى معامل تفاضلي يرد فيها. والمعادلة التفاضلية الجزئية تسمي خطية linear PDE إذا كانت من الدرجة الأولى فقط في المتغير التابع المجهول وجميع مشتقاته الجزئية. ومن أبرز الأمثلة عملياً على معادلات تفاضلية جزئية وخطية من المرتبة الثانية المعادلات الآتية:
المعادلة الموجية وحيدة البعد (∂^2 u)/(∂t^2 )=c^2 (∂^2 u)/(∂x^2 )
المعادلة الحرارية وحيدة البعد ∂u/∂t=k (∂^2 u)/(∂x^2 )
معادلة لابلاس ثنائية البعد (∂^2 u)/(∂x^2 )+(∂^2 u)/(∂y^2 )=0
معادلة بواسون ثنائية البعد (∂^2 u)/(∂x^2 )+(∂^2 u)/(∂y^2 )=f(x,y)
معادلة لابلاس ثلاثية البعد (∂^2 u)/(∂x^2 )+(∂^2 u)/(∂y^2 )+(∂^2 u)/(∂z^2 ) =0
المعادلة التفاضلية الجزئية هي معادلة رياضية تحتوي علي مشتقات جزئية لمتغير تابع أو توابع بالنسبة لمتغيرين مستقلين أو أكثر .
تستخدم المعادلات التفاضلية الجزئية لصياغة وحل المسائل التي تتعلق بتوابع ذات عدة متغيرات مستقلة مثل تلك الموجودة في الصوت والحرارة والكهرباء الساكنة وتدفق الموائع والمرونة وغيرها ، حيث أنه من الممكن التعبير عن ظواهر فيزيائية مختلفة باستخدام معادلات رياضية متشابهة الصيغة.
وتعد مرتبةُ المعادلة order of equation هي مرتبةَ أعلى معامل تفاضلي يرد فيها. والمعادلة التفاضلية الجزئية تسمي خطية linear PDE إذا كانت من الدرجة الأولى فقط في المتغير التابع المجهول وجميع مشتقاته الجزئية. ومن أبرز الأمثلة عملياً على معادلات تفاضلية جزئية وخطية من المرتبة الثانية المعادلات الآتية:
المعادلة الموجية وحيدة البعد (∂^2 u)/(∂t^2 )=c^2 (∂^2 u)/(∂x^2 )
المعادلة الحرارية وحيدة البعد ∂u/∂t=k (∂^2 u)/(∂x^2 )
معادلة لابلاس ثنائية البعد (∂^2 u)/(∂x^2 )+(∂^2 u)/(∂y^2 )=0
معادلة بواسون ثنائية البعد (∂^2 u)/(∂x^2 )+(∂^2 u)/(∂y^2 )=f(x,y)
معادلة لابلاس ثلاثية البعد (∂^2 u)/(∂x^2 )+(∂^2 u)/(∂y^2 )+(∂^2 u)/(∂z^2 ) =0
- معلم: أ. سلمى فتحي
- معلم: أ.م.د. سيد فؤاد
